前言
点差法定义
“点差法”,即差分法,适用于解决直线与圆锥曲线相交的弦的中点问题,回避了使用运算量较大的韦达定理,从而转化为与直线斜率有关的问题。它的本质是两平行方程的变形。
引例:如点\(P(4,2)\)是直线\(l\)被椭圆:\(\cfrac{x^2}{36}+\cfrac{y^2}{9}=1\)所截得的线段的中点,求直线\(l\)的方程。
分析:设直线与椭圆相交于两点\(A(x_1,y_1)\)和\(B(x_2,y_2)\),
由于点\(P(4,2)\)是线段\(AB\)的中点,故有\(x_1+x_2=8\),\(y_1+y_2=4\);
又由于点\(A、B\)都在椭圆上,
则有\(x_1^2+4y_1^2=36①\),\(x_2^2+4y_2^2=36②\),
两式作差得到,\((x_1^2-x_2^2)+4(y_1^2-y_2^2)=0\),
即\((x_1+x_2)(x_1-x_2)+4(y_1+y_2)(y_1-y_2)=0\),
也就是\(\cfrac{y_1-y_2}{x_1-x_2}=\cfrac{-(x_1+x_2)}{4(y_1+y_2)}=-\cfrac{1}{2}\),
即直线\(l\)的斜率\(k=k_{AB}=-\cfrac{1}{2}\),
由点斜式可得直线\(l\)的方程为\(y-2=-\cfrac{1}{2}(x-4)\),整理得到\(x+2y-8=0\)。
此解法简捷漂亮,因其设点求差,故名点差法。
反思总结:在圆锥曲线中涉及中点弦问题时,往往发挥很大作用。自然,上例中的椭圆也可以替换为双曲线,抛物线,圆等曲线。
方法局限性
1、但点差法只可用于解决中心在原点的圆锥曲线,再利用题中其他条件寻找\(x,y,k,m\)(直线截距)间的关系,允许保留一个未知数,多用于解决过定点问题。
2、对于存在性问题(如问到"是否存在一定点过于直线AB?”)要慎用点差法,因为当题中未明说直线与圆锥曲线的相交情况时,若无交点,\(x_1,x_2,y_1,y_2\)就没有了意义,变形式也就不成立了。故即使利用点差法解出定点(当题中相交情况不确定时),也要检验。
检验方法一:把已知直线与圆锥曲线联立,再算判别式是否≥0,若符合,则存在;
检验方法二:把所得弦的中点代入圆锥曲线本身的约束条件中去看是否满足,如在椭圆中弦的中点应满足\(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}<1\);双曲线中满足\(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}>1\);若符合,则存在。
典例剖析:
例1已知椭圆\(\cfrac{x^2}{2}+y^2=1\),求斜率为\(2\)的平行弦的中点的轨迹方程。
解:设弦的两个端点分别为\(P(x_1,y_1),Q(x_2,y_2)\),\(PQ\)的中点为\(M(x,y)\),
则有\(\cfrac{x_1^2}{2}+y_1^2=1\)①,\(\cfrac{x_2^2}{2}+y_2^2=1\)②,
①-②得到,\(\cfrac{x_1^2-x_2^2}{2}+y_1^2-y_2^2=0\)
则有\(\cfrac{x_1-x_2}{2}+\cfrac{y_1-y_2}{x_1-x_2}(y_1+y_2)=0\)
又由于\(x_1+x_2=2x\),\(y_1+y_2=2y\),\(\cfrac{y_1-y_2}{x_1-x_2}=k=2\),
代入上式,得到\(x+4y=0\),
又由于弦中点在椭圆内,故所求的弦中点的轨迹方程为\(x+4y=0\)(在已知椭圆内)。
例7已知点\(M(-1,1)\)和抛物线\(C:y^2=4x\),过\(C\)的焦点且斜率为\(k\)的直线与\(C\)交于\(A\),\(B\)两点,若\(\angle AMB=90^{\circ}\),则\(k\)=_________。
分析:做出如下示意图,连结\(MH\),\(H\)为焦点弦\(AB\)的中点,
由于\(\triangle AMB\)为直角三角形,\(H\)为\(AB\)的中点,则\(MH=\cfrac{1}{2}AB\),
又由于\(AB=AF+BF=AP+BQ\),则\(MH=\cfrac{1}{2}AB=\cfrac{1}{2}(AP+BQ)\),
故\(MH\)为直角梯形的中位线,则\(MH//x\)轴,
设\(A(x_1,y_1)\),\(B(x_2,y_2)\),则有\(y_1^2=4x_1\) ①,\(y_2^2=4x_2\) ②,
①-②得到,\(y_1^2-y_2^2=4(x_1-x_2)\),即\((y_1+y_2)(y_1-y_2)=4(x_1-x_2)\),
则有\(\cfrac{y_1-y_2}{x_1-x_2}=\cfrac{4}{y_1+y_2}\),即\(k=\cfrac{4}{y_1+y_2}\),
又由于\(MH//x\)轴,\(M(-1,1)\),则\(H\)点的纵坐标为1,即\(\cfrac{y_1+y_2}{2}=1\),则\(y_1+y_2=2\),代入上式,
得到\(k=\cfrac{4}{y_1+y_2}=2\).
法2:向量法,设直线\(AB:y=k(x-1)\),由于点\(A,B\)都在抛物线上,故设\(A(4t_1^2,4t_1)\),\(B(4t_2^2,4t_2)\),
联立直线和抛物线,得到\(\left\{\begin{array}{l}{y=k(x-1)}\\{y^2=4x}\end{array}\right.\),消\(x\)得到,
\(y^2-\cfrac{4}{k}y-4=0\),则由韦达定理可知,\(4t_1+4t_2=\cfrac{4}{k}\),\(4t_1\cdot 4t_2=-4\),
即\(t_1+t_2=\cfrac{1}{k}\),\(t_1\cdot t_2=-\cfrac{1}{4}\),
又\(\overrightarrow{MA}=(4t_1^2+1,4t_1-1)\),\(\overrightarrow{MB}=(4t_2^2+1,4t_2-1)\),\(\angle AMB=90^{\circ}\),
则\(\overrightarrow{MA}\cdot \overrightarrow{MB}=0\),即\((4t_1^2+1)(4t_2^2+1)+(4t_1-1)(4t_2-1)=0\),
打开整理得到,\(16(t_1t_2)^2+4(t_1^2+t_2^2)+1+16t_1t_2-4(t_1+t_2)+1=0\),
代入整理得到,\(\cfrac{4}{k^2}-\cfrac{4}{k}+1=0\),即\((\cfrac{2}{k}-1)^2=0\),解得\(k=2\)。
例7【2019届宝鸡文数质检Ⅲ第7题】双曲线\(\cfrac{x^2}{36}-\cfrac{y^2}{9}=1\)的一条弦被点\(P(4,2)\)平分,那么这条弦所在的直线方程为【】
分析:使用点差法求解,设弦的两个端点\(A(x_1,y_1)\),\(B(x_2,y_2)\),则由于两个点都在双曲线上,
故满足\(\cfrac{x_1^2}{36}-\cfrac{y_1^2}{9}=1\)①,且\(\cfrac{x_2^2}{36}-\cfrac{y_2^2}{9}=1\)②,
两式做差得到,\(\cfrac{x_1^2-x_2^2}{36}-\cfrac{y_1^2-y_2^2}{9}=0\),变形得到\(\cfrac{y_2-y_1}{x_2-x_1}\cdot \cfrac{y_2+y_1}{x_2+x_1}=\cfrac{1}{4}\)
又由于\(\cfrac{y_1+y_2}{2}=2\),\(\cfrac{x_1+x_2}{2}=4\),代入上式得到\(k\cdot \cfrac{2}{8}=\cfrac{1}{4}\),故\(k=\cfrac{1}{2}\),
由于弦过点\(P(4,2)\),且斜率为\(k=\cfrac{1}{2}\),求得直线为\(x-2y=0\),故选\(C\).
例16【2019高三理科数学启动卷,2019陕西省二检试卷第16题】已知等腰\(\triangle ABC\)的底边端点\(A\),\(B\)在双曲线\(\cfrac{x^2}{6}-\cfrac{y^2}{3}=1\)的右支上,顶点\(C\)在\(x\)轴上,且\(AB\)不垂直于\(x\)轴,则顶点\(C\)的横坐标\(t\)的取值范围是__________。
分析:设\(A(x_1,y_1)\),\(B(x_2,y_2)\),弦\(AB\)的垂直平分线交\(x\)轴于点\(C(t,0)\),
\(AB\)的中点为\(M(x_0,y_0)\),则\(x_0>\sqrt{6}\),

由题意有\(\cfrac{x_1^2}{6}-\cfrac{y_1^2}{3}=1\)①,\(\cfrac{x_2^2}{6}-\cfrac{y_2^2}{3}=1\)②,两式相减得到,
\((x_1+x_2)(x_1-x_2)-2(y_1+y_2)(y_1-y_2)=0\),于是有\(x_0(x_1-x_2)-2y_0(y_1-y_2)=0\),
即\(k_{AB}=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{x_0}{2y_0}\),又\(k_{MC}=\cfrac{y_0}{x_0-t}\),由\(k_{AB}\cdot k_{MC}=-1\)得到,
\(\cfrac{y_0}{x_0-t}\cdot \cfrac{x_0}{2y_0}=-1\),即\(x_0+2(x_0-t)=0\),则\(t=\cfrac{3x_0}{2}>\cfrac{3\sqrt{6}}{2}\)。
故\(t\in (\cfrac{3\sqrt{6}}{2},+\infty)\)。
例1?【2019高三理科数学模拟训练题】已知斜率为\(2\)的直线\(l\)过抛物线\(C:y^2=2px(p>0)\)的焦点\(F\),且与抛物线交于\(A\),\(B\)两点,若线段\(AB\)的中点\(M\)的纵坐标为\(1\),则\(p\)等于【】
分析:设点\(A(x_1,y_1)\),\(B(x_2,y_2)\),则有\(y_1^2=2px_1\)①,\(y_2^2=2px_2\)②,
两式作差得到,\((y_1-y_2)(y_1+y_2)=2p(x_1-x_2)\),即\(\cfrac{y_1-y_2}{x_1-x_2}\cdot \cfrac{y_1+y_2}{2}=p\),
又线段\(AB\)的中点\(M\)的纵坐标为\(1\),即\(\cfrac{y_1+y_2}{2}=1\),又\(\cfrac{y_1-y_2}{x_1-x_2}=2\),代入上式,
得到\(p=2\),故选\(C\)。
例10【2019届高三理科数学三轮模拟试题】已知椭圆\(C:x^2+\cfrac{y^2}{b^2}=1(b>0,b\neq 1)\)与直线\(l:y=x+m\)交于\(M\),\(N\)两点,\(B\)为上顶点,若\(|BM|=|BN|\),则\(b\)的取值范围为______________。
分析:设\(M(x_1,y_1)\),\(N(x_2,y_2)\),线段\(MN\)的中点\(P(x_0,y_0)\),
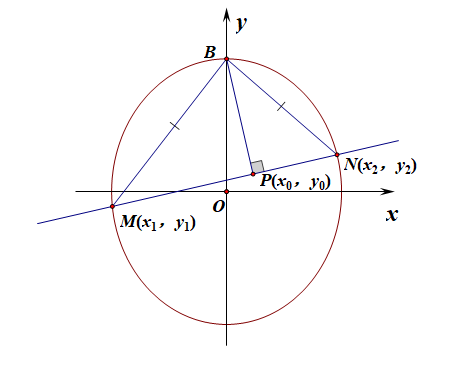
则由\(b^2x_1^2+y_1^2=b^2\)①,\(b^2x_2^2+y_2^2=b^2\)②,且有\(\cfrac{y_2-y_1}{x_2-x_1}=1\),
由点差法,①-②得到,\(b^2(x_1+x_2)=-(y_1+y_2)\),即\(x_0b^2=-y_0\)③,
又\(|BM|=|BN|\),则\(BP\perp MN\),\(k_{BP}=-1=\cfrac{y_0-b}{x_0}\)④,
由③④可得,\(x_0=\cfrac{b}{1-b^2}\),\(y_0=\cfrac{b^3}{1-b^2}\),由于点\(P(\cfrac{b}{1-b^2},\cfrac{b^3}{1-b^2})\)在椭圆内,
故\(\cfrac{b^2}{(1-b^2)^2}+\cfrac{\frac{b^6}{(1-b^2)^2}}{b^2}<1\),
解得\(3b^2<1\),又\(b>0\),故\(0<b<\cfrac{\sqrt{3}}{3}\)。
解后反思:①出现这种范围问题的求解策略,其一,联立求解\(\Delta >0\);其二,点\(P(x_0,y_0)\)在椭圆内,则\(\cfrac{x_0^2}{a^2}+\cfrac{y_0^2}{b^2}<1\),
②涉及到与圆锥曲线相交的直线的斜率、中点问题常常考虑使用点差法。
反例提升
反例如点\(P(4,2)\)是直线\(l\)被椭圆:\(\cfrac{x^2}{4}+y^2=1\)所截得的线段的中点,求直线\(l\)的方程。
分析:设直线与椭圆相交于两点\(A(x_1,y_1)\)和\(B(x_2,y_2)\),
由于点\(P(4,2)\)是线段\(AB\)的中点,故有\(x_1+x_2=8\),\(y_1+y_2=4\);
又由于点\(A、B\)都在椭圆上,
则有\(x_1^2+4y_1^2=4①\),\(x_2^2+4y_2^2=4②\),
两式作差得到,\((x_1^2-x_2^2)+4(y_1^2-y_2^2)=0\),
即\((x_1+x_2)(x_1-x_2)+4(y_1+y_2)(y_1-y_2)=0\),
也就是\(\cfrac{y_1-y_2}{x_1-x_2}=\cfrac{-(x_1+x_2)}{4(y_1+y_2)}=-\cfrac{1}{2}\),
即直线\(l\)的斜率\(k=k_{AB}=-\cfrac{1}{2}\),
由点斜式可得直线\(l\)的方程为\(y-2=-\cfrac{1}{2}(x-4)\),整理得到\(x+2y-8=0\)。
易知上例中,点\(P(4,2)\)在椭圆:\(\cfrac{x^2}{4}+y^2=1\)的外边,故点\(P(4,2)\)绝不可能是弦\(AB\)的中点,
此时点差法显的有点尴尬无奈。可见,点差法只能解决真正的中点问题,对于需要判别的情况应先判别再应用。